Markov Decision Processes - The Framework For Decision-Making Under Uncertainty

Finite Markov Decision Processes (MDPs) are fundamental processes in reinforcement learning (RL) and are an extension of markov chains, systems where the next state is only dependent on the current state. MDPs extend Markov chains by simply adding in actions and rewards, hence turning a stochastic process into a stochastic decision process. They are useful for studying optimization problems solved using dynamic programming, which is a method for solving problems with optimal substructure, that is, where the optimal solution to a problem can be found by combining optimal solutions to its subproblems. In this post, we'll go over the basics of MDPs and how they are used in RL.
MDPs involve both evaluative feedback, as with the k-armed bandits, but also an associative aspect, where actions influence not just immediate rewards, but also subsequent situations (or states). This leads to delayed rewards and the need to trade off immediate and delayed rewards because the state the bot finds itself in can impact future rewards. In this sense, the RL agent is trying to determine how both their environment and actions map onto value. In k-armed bandits, the goal is to estimate the value $q_{*}(a)$ of each action $a$, while with MDPs, the goal is to estimate $q_{*}(s,a)$ of each action $a$ in each state $s$, or the value $v_{*}(s)$ of each state given optimal action selections. It's important to not that MDPs are a mathematically idealized form of the RL problem.
The agent-environment interface is the foundation of MDPs. The agent, or the learner and decision maker, interacts with the environment, which presents new situations and gives rise to rewards that the agent seeks to maximize over time with its actions. The agent and environment interact at discrete time steps $t=0,1,2,3,...$ and at each time step, the agent receives a representation of the environment's state, $S_t \in S$ and from that, selects an action, $A_t \in A(s)$. One time step later, the agent receives a reward $R_{t+1} \in R$ and finds itself in a new state $S_{t+1}$. The state space can be anything including stock returns, the score of a game, or the position of a robot. A common diagram used to represent this, as well as RL in general, is the following:
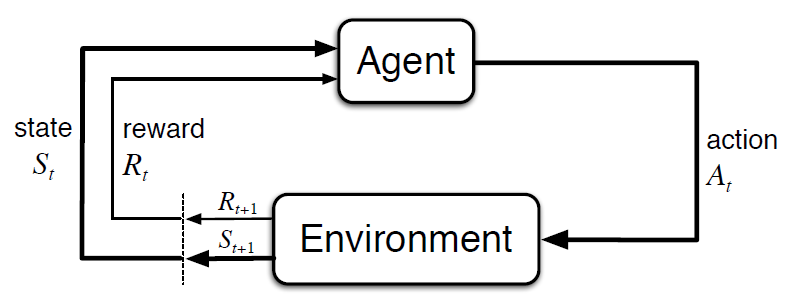
In a finite MDP, the sets of states, actions, and rewards ($S, A, R$) all have a finite number of elements. In this case, the random variables $R_t$ and $S_t$ have well defined discrete probability distributions dependent only on the preceding state and action. The state-transition probabilities can be computed as:
$$p(s'|s,a) \coloneqq Pr(S_t=s'|S_{t-1}=s,A_{t-1}=a) = \sum_{r \in R}p(s',r|s,a)$$and the expected rewards for state-action pairs can be computed as:
$$r(s,a) \coloneqq \mathbf{E}[R_{t}|S_{t-1}=s,A_{t-1}=a] = \sum_{r \in R}r\sum_{s' \in S}p(s',r|s,a)$$The general rule is that whatever cannot be changed by the agent is considered part of its environment. However, the reward computation is always considered external to the agent because it defined the task facing the agent and is beyond its ability to change arbitrarily. The agent-environment boundary represents the limit of the agent's absolute control, not of its knowledge.
Sources¶
Sutton, R. S., Barto, A. G. (2018). Reinforcement learning: An introduction (2nd ed.). MIT Press Ltd.
White, M., White, A. (n.d.). Reinforcement Learning Specialization [MOOC]. Coursera.
Markov Chains | Brilliant Math & Science Wiki. (n.d.). Brilliant.org. https://brilliant.org/wiki/markov-chains/#:~:text=A%20Markov%20chain%20is%20a
Wikipedia Contributors. (2019, May 20). Markov decision process. Wikipedia; Wikimedia Foundation. https://en.wikipedia.org/wiki/Markov_decision_process
